Notes from ANU ASTRO1x - The Greatest Unsolved Mysteries of the Universe

Last Updated: March 29, 2025

Note: These notes are from Ongoing Course. I will update them as I go along. Hopefully, completing before the sun becomes a red giant.

1. The Expanding Universe

1. The Expanding Universe

Vesto Slipher was the first to observe shifts in spectral lines in spiral nebulae in 1912, measuring their redshifts . Later, Edwin Hubble built upon this with his distance-redshift relation (Hubble’s Law) in 1929, laying the foundations of Modern Observational Cosmology.

1.1 Distances in Astrophysics

Distance is everything in astrophysics.

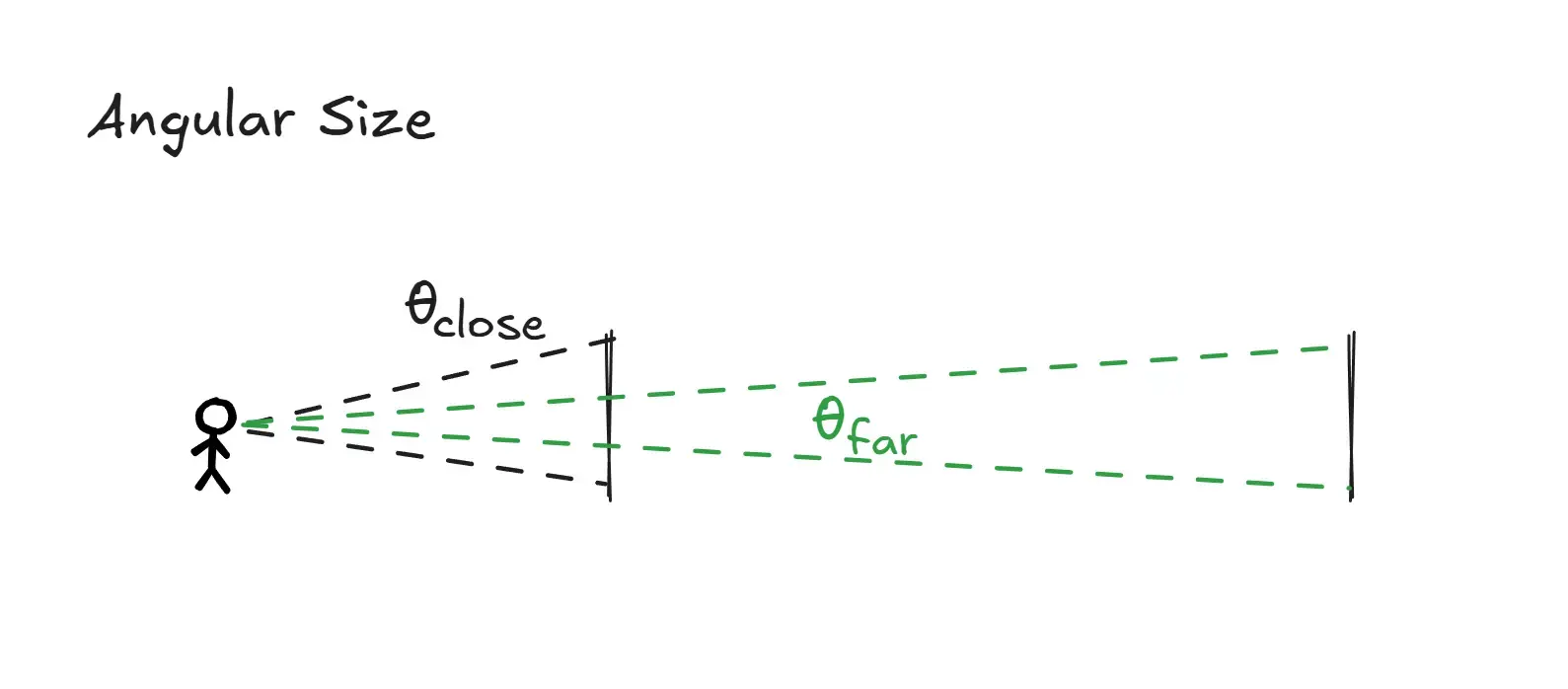
Angular size is how large an object appears in the sky from a point of observation

For small angles (which works well in astrophysics for galaxies, stars, etc.),

\theta = \frac{l}{r}

where, $\theta$ = angular size (in radians),
$l$ = actual (physical) size of the object,
$r$ = distance to the object from the observer.

Units of Angular size : 1 full circle = 360°.
$1° = 60'(arcminutes) = 3600 ''(arcseconds)$

Angular size is inversely proportional to distance. If an object moves further away, its angular size decreases. $\theta \propto \frac{1}{r}$

Angular Size inversely proportional to distance

The Moon and Sun both have about the same angular size 0.5 degree. The Sun is 400 times larger than the Moon, but also 400 times further away. Thus making them appear the same size, and giving us the beautiful phenomenon of total Solar Eclipse. Angular size helps us estimate distances in astrophysics when the actual size is known.

Arc Length
If we imagine our view of sky as a circle, and the angular size theta is a fraction of the circle. Arc length will be the circumference of the circle times the fraction.

S = {2\pi r} \times \frac{\theta}{360°}

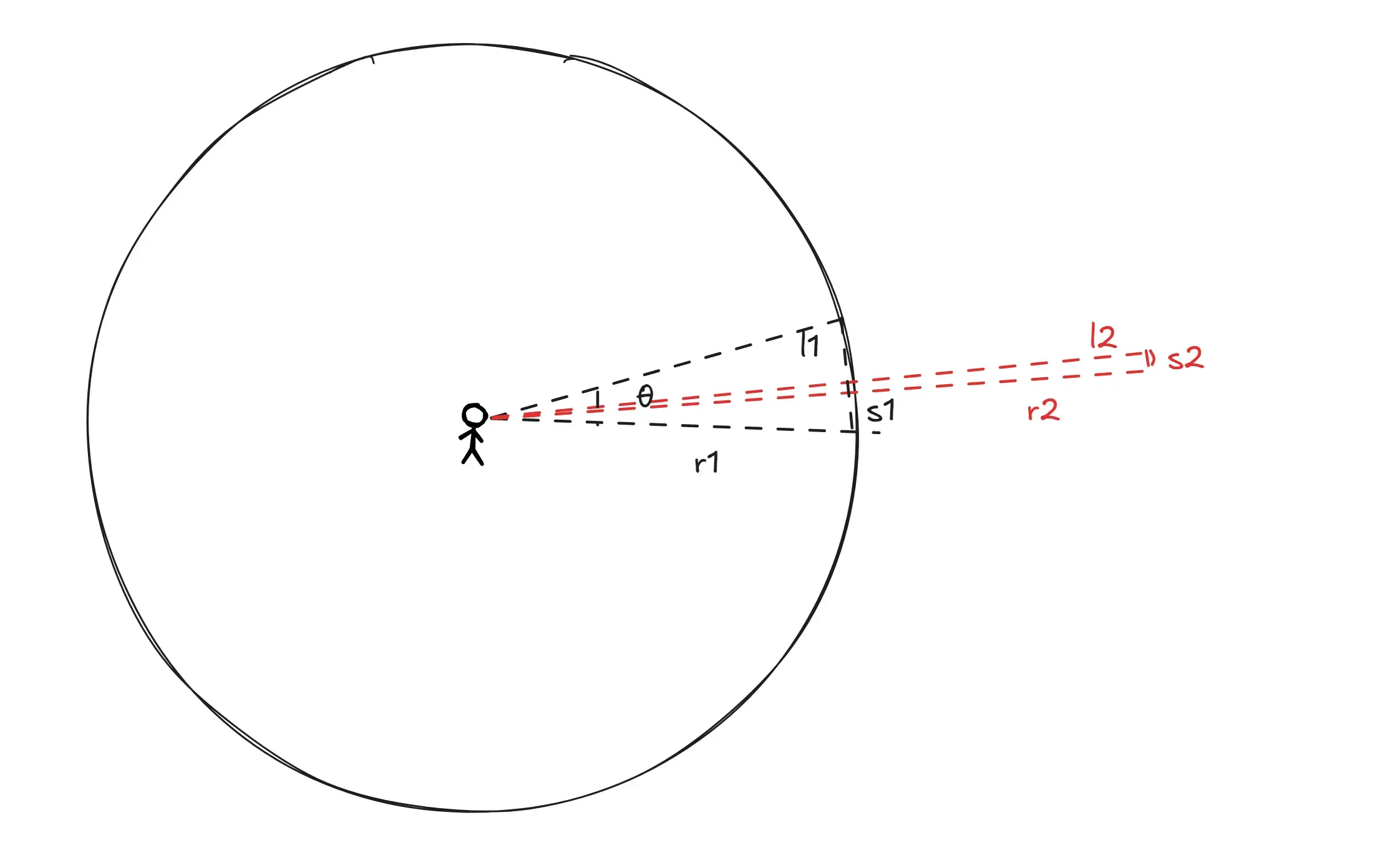
where, $S$ = arc length, $2\pi r$ = circumference of the circle, $\frac{\theta}{360°}$ = fraction of the angular size $\theta$ of the circle.

To convert degree to radians, we use the following formula:

2\pi \text{ radians} = 360\\ 1 \text{ radian} = \frac{360}{2\pi} = \frac{180}{\pi}

or alternatively,

1° = \frac{\pi}{180} \text{ radians}

When we are dealing the large objects but very small angular size, as if the circle becomes the too large and theta gets smaller, in that case, $S = l$ .
Imagine, you zoom in a part of circumference of of a very big circle, in that case, the arc length would be near equal to the chord length, e.g. the distance between two points on the circumference of the circle.

so, when dealing with large distances, $r >> l$ ,

S = l = 2\pi r \times \frac{\theta}{360°} \\ = r \times \cancel{360°} \times \frac{\theta}{\cancel{360°}} \\ = r\theta (\theta \text{ in radians} )

Length of an object is its distance times the angular size

1.2 Flux, luminosity and distance

Luminosity: total amount of energy emitted by an object per unit time (second) in all directions. Measured with Watts(W). It’s an fundamental property of an object (it doesn’t change with distance).

Flux: amount of energy per unit area per second received from an object. Measured by Watts per square meter ( $W \cdot m^{-2}$ ). Flux decreases with distance, because the same amount of energy gets spread over a large area. Flux is what measures an object in space. From $F = \frac{L}{4\pi r^2}$ , we get the luminosity (provided we get distance from elsewhere)

In the following equation, $F$ is the flux, $L$ is the luminosity, and $r$ is the distance. $A$ is the surface area of a sphere with radius $r$ . The total luminosity ( $L$ ) of a source is spread spherically in all directions. The energy emitted per second is distributed over a sphere with radius $r$ . The surface area of this sphere is $A =4\pi r^2$ .

F = \frac{L}{A}\ = \frac{L}{4\pi r^2}

From the above equation, $L$ stays the same, as total energy emitted per second is constant. $4\pi$ is a constant.

F = \frac{L}{4\pi} \cdot \frac{1}{r^2} \\ F \propto \frac{1}{r^2}

Flux is inversely proportional to the square of the distance. Further something is, dimmer it is.

1.3 Spectra

Electromagnetic Spectrum represents the wavelength of waves, starting from the Gamma ray $10^{-9}$ m, to X-ray, UV, the Visible Spectrum, Infrared, Microwave, and Radio Waves $10^3$ m.

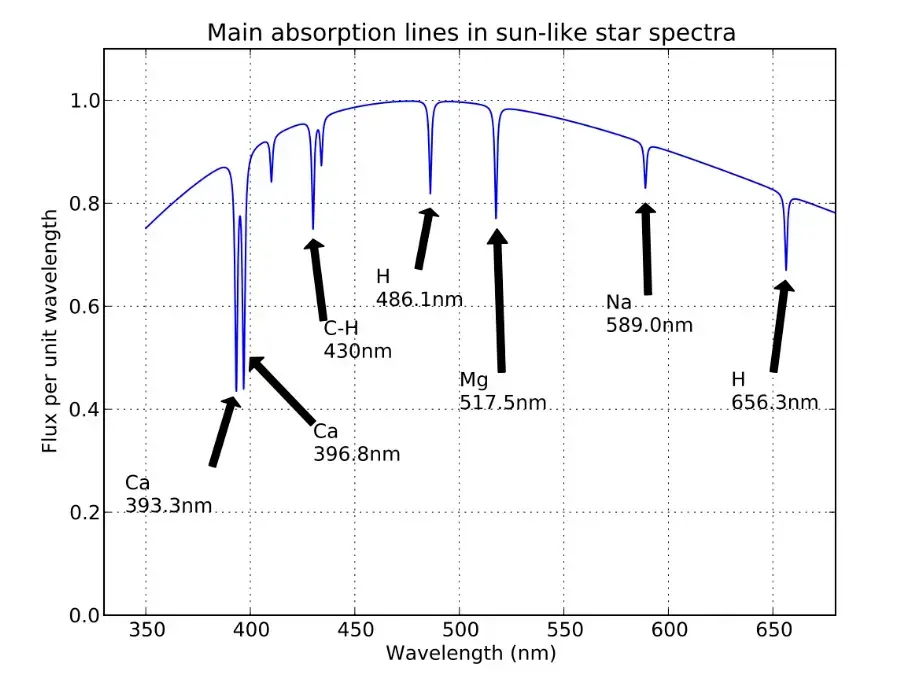
The Visible Spectrum falls at the wavelength range of $380 - 750$ nm or $380 - 750 \times 10^{-9}$ m. Violet is at $380$ nm and Red is at $750$ nm.

From the spectra, we can determine the elements present in the source object, observing the absorption lines. As each elements have unique absorption lines. Spectral graphs is also used to measure redshifts, by measures shift in wavelength, using the concept of Doppler Effect.

1.4 Doppler Effect

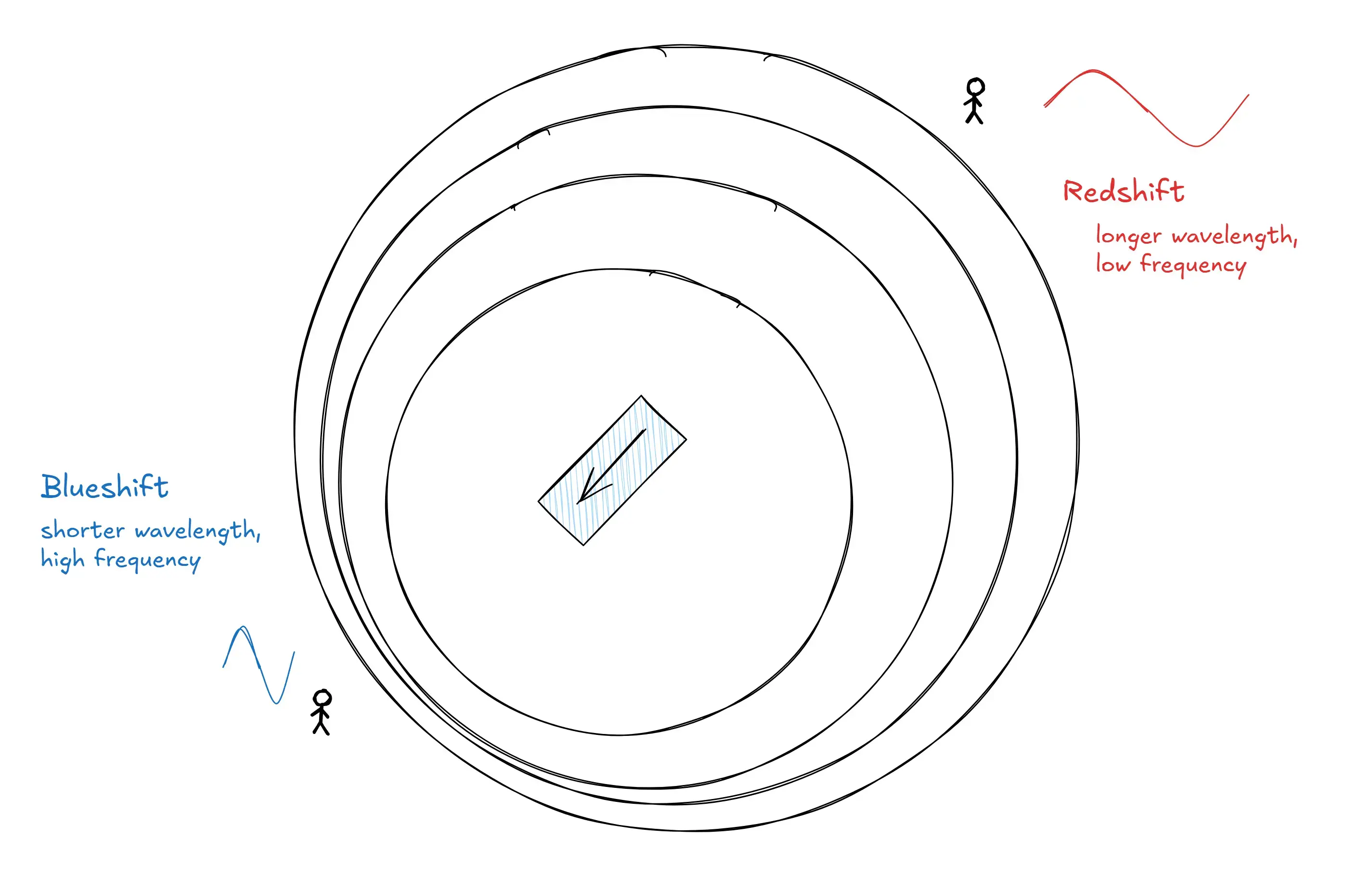
We're surrounded by waves. Sound waves, light waves (electromagnetic waves). Doppler effect happens when source of the wave moves relative to the observer. When the source object moves towards the observer, it compresses the wave moving forward, creating shorter wavelength, while moving away from the observer, it stretches the wave, creating longer wavelength. Shorter wavelength is high frequenct as frequency is inversely proportional to wavelength.

f = \frac{v}{\lambda}

where, $f$ = frequency, $v$ = velocity of the wave, $\lambda$ = wavelength.

From the electromagnetic spectrum, blue lies at shorter wavelength and red lies at longer wavelength. Hence, the blue shift is when the wavelength decreases and red shift is when the wavelength increases. In other words, blue shifted when the object is coming towards us and red shifted when the object is moving away from us.

How to measure doppler shift using spectra

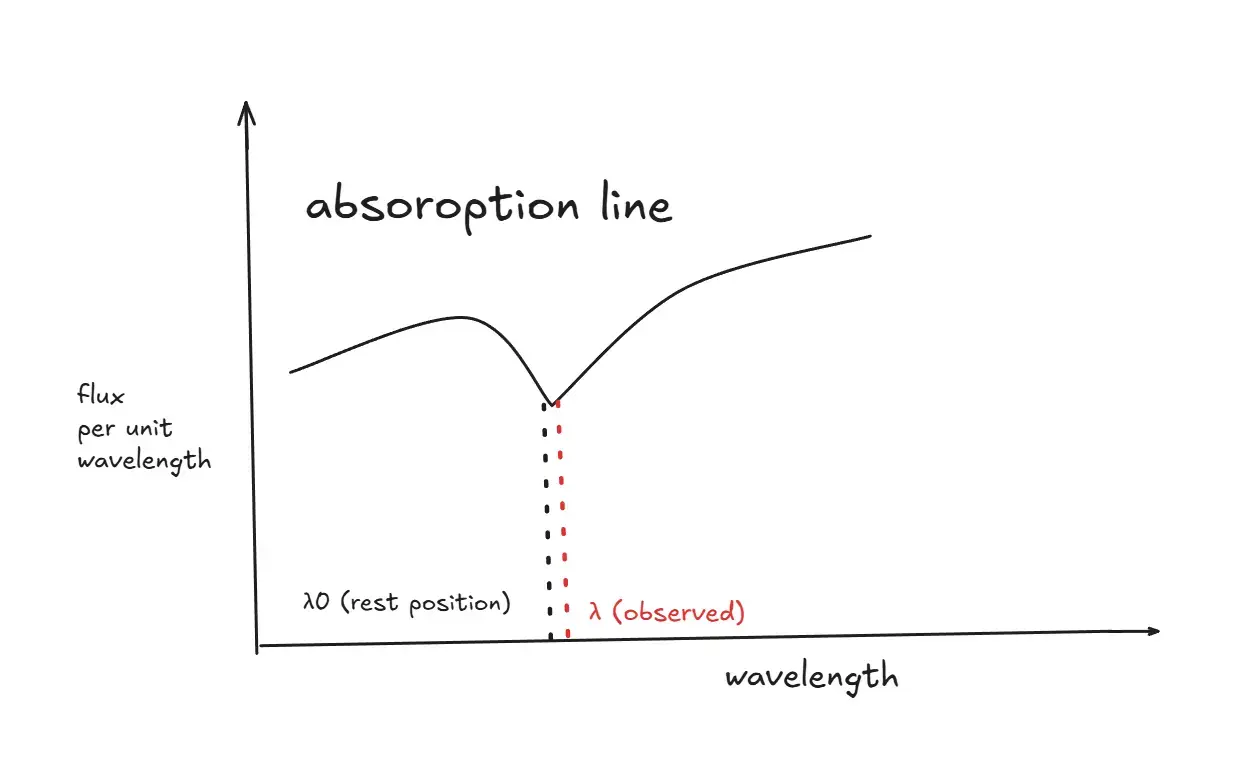
The Doppler effect in spectra is measured by observing the shift in the wavelength of spectral lines from their known rest positions.

shift, $\Delta \lambda = \lambda - \lambda_0$

where, $\lambda$ = observed wavelength, $\lambda_0$ = rest wavelength.

Calculating the redshift, $z = \frac{\Delta \lambda}{\lambda_0}$

If $z > 0$ , the object is redshifted (moving away).

If $z < 0$ , the object is blueshifted (moving closer). also expressed as negative redshift.

When the velocity of the object is much less than the speed of light, we can use the non-relativistic formula,

z \approx \frac{v}{c}

This is derived from the classical Doppler effect:

\lambda_{obs} = \lambda_{emit} \left(1 + \frac{v}{c}\right)

which gives:

z = \frac{\lambda_{obs} - \lambda_{emit}}{\lambda_{emit}} = \frac{v}{c}

When the velocity of the object is close to the speed of light ( $v \approx c$ ), we need to use the relativistic formula,

1+z= \frac{1+v/c}{1-v/c}

z= \frac{1+v/c}{1-v/c} - 1

1.5 Hubble Law

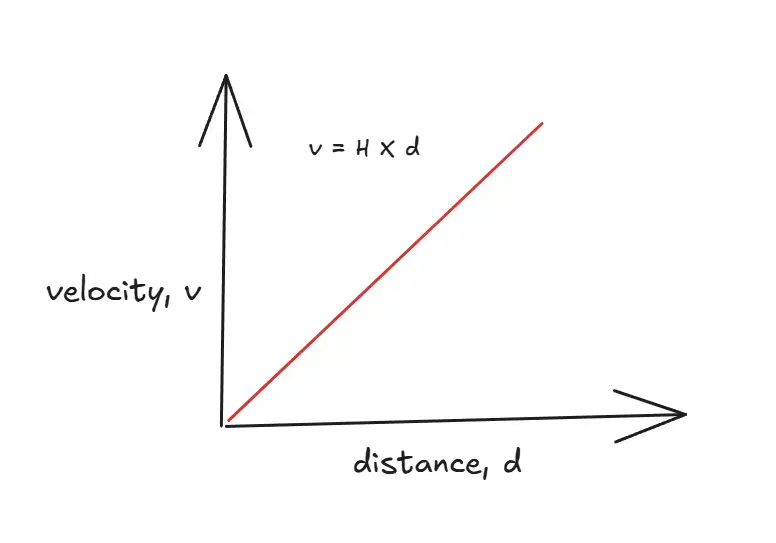
Hubble’s Law states that galaxies move away from us at speeds proportional to their distance, due to the expansion of the universe.

The universe is expanding, everything is moving away from everything else. Like a blowing up a ballon, the points are moving away from each other.

Observing the redshift of galaxies, the law was postulated.

v = H_0 \times d

where, $v$ = velocity of the galaxy (recessional velocity, km/s), $d$ = distance of the galaxy (Mpc), $H_0$ = Hubble constant (70 km/s/Mpc).

Discovered in 1929 by Edwin Hubble.

Further the galaxies are moving away from us, the faster the recessional velocity.

1.6 Steady State Theory vs Big Bang

In 2004, Hubble Space Telescope captured the image of the Hubble Ultra deep field, which is the farthest image ever taken by Hubble telescope.

It captured the image of galaxies from 13 billion years ago, showing the infancy of the universe.

Big Bang is an explosion OF space, not an explosion IN space.

Space itself is expanding, and everything within it is affected by this expansion.

Objects that are far apart, with little matter in between, are moving away from each other at an increasing rate due to the accelerated expansion of the universe (driven by dark energy).

Objects bound together by atomic, chemical, or gravitational forces are not expanding because these forces are strong enough to resist the expansion of space.

Steady State Theory

proposed in the late 1940s by Fred Hoyle, Thomas Gold, Hermann Bondi, and others.

Suggested that the universe has no beginning or end in time and maintains a constant overall appearance

As the universe expands, new matter is continuously created to keep the density of the universe constant. But this violates the conservation of mass & energy.

It states the universe looks the same at all times and in all directions, no matter where you are or when you observe it. extending the Cosmological Principle, which says the universe is homogeneous and isotropic on large scales, by adding time invariance (unchanging over time).

So, we have two contradictory theories.

Big Bang Theory: universe should have decreasing density. Volume increases as the space expands. If we follow the conservation of mass & energy, the mass should remain same. Thus, from $\rho = \frac{m}{V}$ , as $V$ increases, $\rho$ decreases.

Steady State Theory: universe should have constant density. It should look the same at all times and in all directions.

Thus, if we can prove anything changing at all, Big Bang Theory is wins.

1.7 Quasars, Cosmic Microwave Background Radiation and Big Bang

Quasars

Quasars (quasi-stellar radio sources) are found at the core of distant galaxies, powered by supermassive black holes at the center.

It's among the most luminous objects in the universe, and they outshine entire galaxies to due to matter falling into the accretion disk around the black hole.

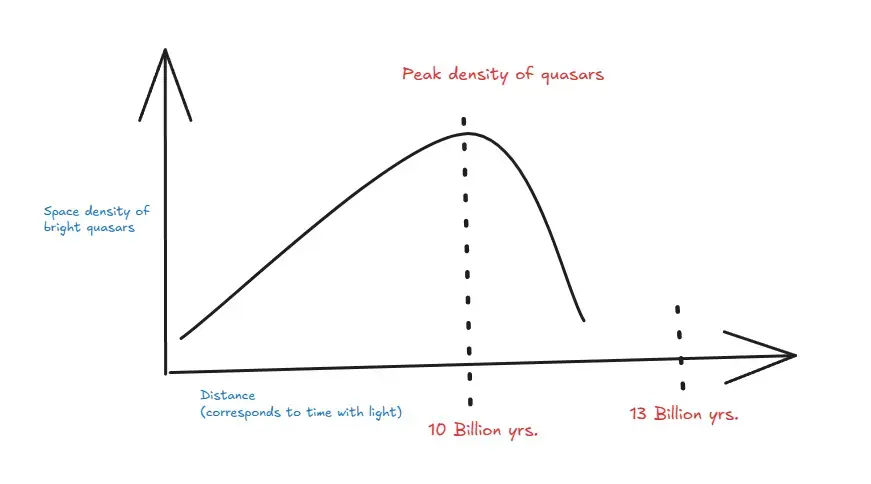
Quasars are the most distant objects in the universe, and they are the most luminous objects in the universe.

Quasars are redshifted, they are found in early universe, far far away, when universe was denser, when early galaxies had more gas available for feeding black holes, making quasars more common.

As galaxies evolved, gas was used up, leading to fewer active quasars today.

Modern galaxies, including the Milky Way, have dormant supermassive black holes that are not currently feeding enough to become quasars.

The Closest Known Quasar: 3C 273 (in the Virgo constellation). ~2.4 billion light-years (750 Mpc) away. Identified in 1963.

Cosmic Microwave Background(CMB)

Today's universe doesn't emit microwaves. In the early universe (about 380,000 years after the Big Bang), the universe was extremely hot and dense. As the universe expanded, it cooled until it reached about 3000 K. At this temperature, electrons and protons combined to form neutral hydrogen (a process called recombination). Without free electrons to scatter photons, light was free to travel for the first time. This released a "glowing wall of light", which we now see as the Cosmic Microwave Background (CMB).

We will come to "photon-baryon plasma" stage" later in the course

This light was high-energy visible and infrared radiation. However, as the universe expanded, the wavelength of the light increased, and shifted into the microwave region of the electromagnetic spectrum.

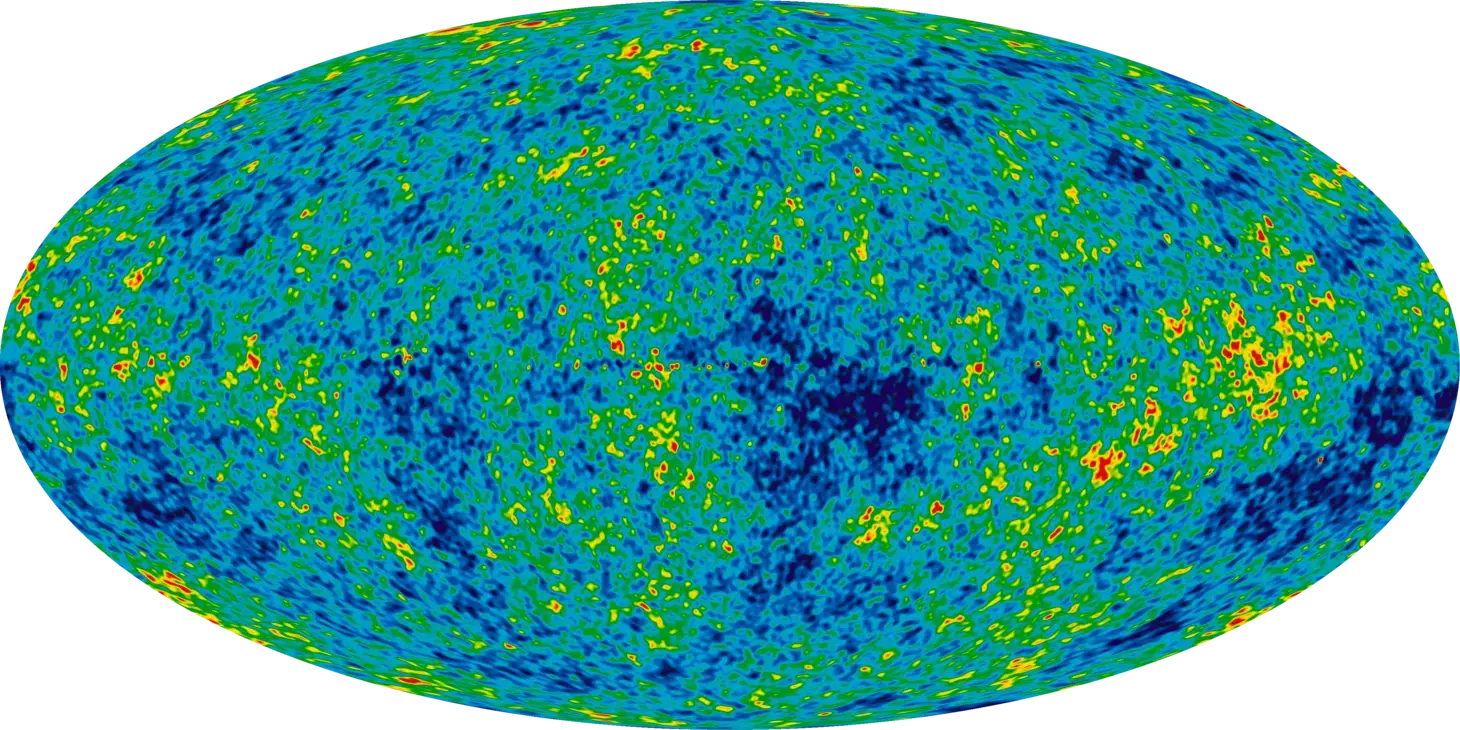
Thus, Quasars and CMB proves the universe is expanding and changing over time. And Big Bang Theory is correct.

1.8 Blue Shifted Galaxies

As per Hubble's Law, everything is expanding, thus the we should observe red shift in galaxies.

However, when we observe our nearest galaxy. Andromeda (M31), we see it is blue shifted.

The reason is for this pecularity is, the gravitional pull between Andromeda and Milky Way is stronger than the expansional pull of the universe. Thus, they are moving towards each other.

Andromeda is expected to collide with the Milky Way in about 4.5 billion years.

Often times, galaxies merge together forming bigger galaxies.

Further apart galaxies are, less affected by the gravitational pull, following Newton's inverse square law.

Turnaround Radius: the maximum radius at which a gravitationally bound system (like a galaxy cluster) can resist the expansion of the universe. Beyond this radius, the cosmic expansion dominates, pulling objects apart. The value is around 20 million light years or (~6 Mpc). However, this value depends on the mass of the objects.

(TO BE CONTINUED...)

Table of Contents